L'avantage du service

Si l’on regarde en détail le résultat de matches de tennis entre joueurs de même force, on peut remarquer deux fait apparemment contradictoires :

• Une importante majorité des jeux sont remportés par le serveur (au moins 75%)
• Le serveur remporte à peine plus de la moitié des points.

Ces deux faits sont-ils compatibles en termes de probabilité, c’est-à-dire suffit-il de gagner 60% des points pour gagner plus de 75% des jeux, ou bien y a-t-il une raison particulière qui fait que le relanceur gagne moins de jeux qu’il ne le devrait, par exemple une question d’endurance ?

Faire le calcul en détail, par les moyens de la combinatoire, serait d’une complexité extrême, d’autant que le nombre de possibilités est infini (le nombre de points d’un jeu n’est limité par rien).

On peut réaliser un modèle graphique de l’évolution d’un jeu ; les intersections représentant les scores possibles, et les flèches représentant le fait qu’un résultat peut conduire à un autre au point suivant ; toute transition est affectée d’une probabilité p  si elle résulte du gain d’un point par le serveur, et 1-p  si elle résulte du gain d’un point par le relanceur. Ce qui peut très facilement être transcrit dans un tableur, qui nous donnera, pour chaque valeur de p , probabilité de gain d’un point, une valeur de la probabilité de gain d’un jeu.

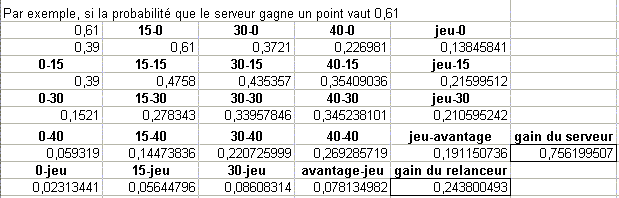
Ceci donne, pour une valeur de p  de 61%, une probabilité, pour le serveur, de plus de 75% de gagner le jeu. Les observations ci-dessus sont donc parfaitement plausibles.