
Les symétries dans
l'art
 |
Les symétries dans
l'art |
Contenu de ce document
N'hésitez pas à cliquer sur les miniatures; elles ouvrent une nouvelle page avec l'image en grand format.
Nous allons nous intéresser dans ces pages à la symétrie de certains objets relevant de l’Art sous plusieurs de ces formes. Avant tout, il faut clarifier les termes "symétrie d’un objet". Pour le mot "symétrie", le Larousse nous rappelle qu’il s’agit d’une "transformation qui, à un point M, fait correspondre un point M’ tel que le segment MM’ possède soit un seul point fixe comme milieu (symétrie par rapport à un point), soit une droite ou un axe fixe comme médiatrice (symétrie par rapport à une droite, à un axe), ou encore un plan fixe comme plan médiateur (symétrie par rapport à un plan)". Nous reconnaissons dans ces quelques lignes les transformations qui nous ont été enseignées dans le secondaire sous les noms de symétrie centrale dans le plan, symétrie bilatérale - ou orthogonale - dans le plan, et symétrie planaire dans l’espace. Toutefois, nous allons approcher l’idée de symétrie d’une notion plus vague, plus intuitive. Nous dirons qu’un objet est symétrique s’il est vu de manière identique sous des angles de vues différents.
Nous prendrons comme premier exemple le cube. Lorsque vous tenez un cube en main, il existe 48 points de vues différents qui vous restitueront son image fidèle. Une partie de ces points de vue est constituée de la symétrie centrale et de quelques symétries orthogonales dont les plans de symétries sont parallèles aux faces, ou bien traversant deux arêtes opposées. Mais en combinant ces symétries planaires, nous allons construire des rotations. Il n’est pas bien difficile d’imaginer qu’en tournant votre cube de quarts de tours dans plusieurs sens, vous retrouverez sa forme de départ. Le cube est donc constitué de 48 symétries.
Dans l’ensemble de ce document, nous nous intéresserons aux symétries suivantes: Symétries centrales et orthogonales, rotations, translations, et homothéties. Nous ne nous attarderons pas trop sur cette dernière qui n’a pas, à la différences des autres, la propriété de conserver les mesures de l’objet considéré.
Nous devrons également formaliser nos propos et définir clairement nos outils. Ainsi, nous éviterons le terme symétrie, et le remplacerons par le mot "automorphisme". De même, un automorphisme ne s’applique pas à un "objet", mais bien à un "ensemble structuré". Dans le cadre du cube, il n’est pas difficile de le voir comme une ensemble constituée de 8 sommets, structurés entre eux par l’adjacence de sommets.
Soient E et E’ deux ensembles structurés. Nous définissons un isomorphisme de E sur E’ comme une bijection a telle que a transforme la structure de E en celle de E’ .
Un automorphisme de E est un isomorphisme de E sur lui-même. Nous le notons Aut(E),° .
Un groupe de permutations sur un ensemble E est un ensemble G de permutations des
éléments de E tel que
1. Si b et a sont dans G, alors b ° a est dans G.
2. Si a est dans G, alors a -1 est dans G.
3. La permutation identique 1E est dans G.
Observons que Aut(E),° est un groupe de permutations.
Si En est l’espace euclidien de dimension n, une isométrie de En est une permutation a des points de En qui conserve les distances. L’ensemble de toutes les isométries de En forme un groupe de permutation noté Iso(En),° .
Voici en trois théorèmes la classification des isométries de E1 , E2 ,et E3:
1. Toute isométrie de la droite euclidienne E1 est
une translation
une symétrie centrée.
2. Toute isométrie du plan euclidien E2 est
une translation
une rotation autours
d’un point (dont la symétrie centrée est un cas particulier)
une symétrie glissée
(une symétrie orthogonale suivie d’une translation parallèle à l’axe de
symétrie).
3. Toute isométries de l’espace euclidien E3 est
un vissage,
déplacement hélicoïdal
une symétrie glissée,
composition d’une symétrie planaire et d’une translation parallèle au plan
une antirotation,
composition d’une symétrie planaire et d’une rotation autour d’un axe
perpendiculaire au plan
Nous remarquons, comme annoncé précédemment, que les homothéties ne figurent pas dans la liste des isométries puisqu’elles ne conservent pas les mesures de l’objet. L’aspect "symétrique" qu’elles procurent n’est pourtant pas à dédaigner. Malgré cela, les exemples d’homothéties dans l’Art ne sont pas légion. Un petit exemple vous permettra de voir de quoi il s’agit en observant les deux étages supérieurs du pont du Gard, l’aqueduc romain situé dans le Vaucluse, en France.
En effet, le dernier étage à la "même forme" que l’étage central, avec une différence nette dans la taille des arches. Ainsi, il existe plusieurs centres d’homothéties situés sur le dessus du pont qui envoient toute arche du dernier étage sur toute arche de l’étage central.
Un autre exemple, architectural ou descriptif, peut être aperçu dans la plupart des représentations de la tour de Babel, parmi lesquelles celle de Brueghel.
Il a été dit que la source du mythe de cette tour de Babel était la Zigourat de Babylone. Sans confirmer cette hypothèse, notons que la forme des Zigourat est en effet très proche d’une figure conservée par des homothétie.
Terminons cette parenthèse sur la tour de Babel en vous montrant une représentation de l’édifice qui serait conservé, non pas par homothéties, mais par translation. En considérant l’aspect infini de ce batîment, il s’agira même du seul exemple de ce site vous exposant un cas de groupe de translation infini.
Si la construction de figures homothétiques est intentionnelle, celle par symétrie orthogonale n’est souvent due qu’à un besoin esthétique. L’homme est lui-même symétrique suivant un axe vertical, il semble donc normal de le confronter à des objets admettant des symétries d’axe vertical. Il s’agit d’ailleur de la seule symétrie parmi celles que nous citons dont l’homme soit l’objet. Ainsi, une quantité indénombrable de monuments et batiments, et pas des moindres, ont été batis sur ce principe. Nous proposons quelques exemples en dimension 3.
Le premier est le chateau de Versaille. Notons que pour admirer la symétrie d’une telle surface, il faut déjà un certain recul, et qu’à l’époque de sa construction, l’aéronautique n’existait pas. Objectivement, seuls les plans de la construction ou une vue de la facade permettaient de noter la symétrie ici présente.
La beauté de la symétrie ne doit pas forcément faire appel à des détails minutieux. Voyons par exemple l’entrée du temple de Ramses II à Abu Simbel. Les statues ne sont pas identiques, mais forment dans l’ensemble de grandioses symétries.
L’Eglise s’est aussi emparée de la symétrie bilatérale. Commençons par l’allure des cathédrales et églises. Rares sont ces monuments qui ne possèdent pas cette symétrie. A nouveau, la symétrie ne va pas jusque dans les détails: les gargouilles, Saints, anges et autres ne sont pas dédoublés, mais l’apect général est préservé.
Outre les batiments, l’Eglise utilise également la symétrie bilatérale au travers des polyptiques, ces panneauxpeints ou sculptés liés entre eux. Nous passons ici aux symétries à deux dimensions. La remarque faite plus haut reste toutefois valable; le polyptique présenté est symétrique dans sa forme, dans les lieux, les actions, dans les types et nombres de personages, ..., mais pas dans les détails.
Voyons enfin un exemple de symétrie bilatérale dans la musique, le seul art figurant ici n’appartenant pas au domaine des arts plastiques. Notre exemple propose une symétrie bilatérale appliquée à une écriture, ici l’écriture d’une partition. L’initiateur n’est autre que J.-S. Bach, et son oeuvre est l’Offrande Musicale.

Les deux portées de ce morceau sont les symétriques l’une de l’autre. Malgré cet artifice d’écriture, la mélodie qui en ressort est tout-à-fait harmonieuse. Signalons par ailleurs que ce morceau n’est pas la seule contribution de Bach aux mathématiques.
Considérons G un groupe quelconque. Soit x , une partie du groupe G. Soit <x> le sous-groupe engendré par x. Un groupe est dit cyclique s’il est engendré par un seul élément, c’est-à-dire s’il existe un élément a de G tel que G = <a>. L’exemple de groupe cyclique que nous illustrerons est constitué des rotations du plan euclidien E2 qui conserve un n-gone régulier convexe. Nous notons ce groupe Cn. Remarquons que le choix de l’adjectif "cyclique" est dû à ce groupe de rotation.
Voici le théorème de classification des groupes cycliques:
1. Si G est un groupe cyclique fini, alors il est isomorphe à Zn,+.
2. Si G est un groupe cyclique infini, alors il est isomorphe à Z,+.
Nous reviendrons sur cette deuxième partie du théorème lors de l’exposé sur les
frises.
Les exemples de symétries de rotation sous forme cyclique dans l’art sont assez rares. On les retrouve toutefois chez Escher dont nous reparlerons plus tard.
Le groupe des rotations n’est pas le seul groupe à conserver le n-gone régulier convexe. Nous en générons un autre à partir de deux symétries bilatérales du n-gone. Ce nouveau groupe contiendra le groupe des n rotations décrit ci-dessus, ainsi que n symétries bilatérales. Ce groupe sera appelé groupe diédrique, et sera noté D2n.
Voici le théorème de classification des groupes diédriques:
1. Si G est un groupe diédrique fini, alors il est isomorphe à D2n.
2. Si G est un groupe diédrique infini, alors il est isomorphe à D![]() .
.
A nouveau, nous reviendrons sur cette deuxième partie du théorème lors de
l’exposé sur les frises.
Les applications de groupes diédriques dans l’art sont plus courantes. Nous y retrouvons Escher.
En trois dimension, c’est surtout dans les cathédrales que ce retrouvent ces "symétries de rotation". Voici par exemple la rosace de la Cathédrale de Chastres, la coupole de la Cathédrale Santa Maria Della Salute à Venise (extérieur et intérieur), la coupole de la Basilique St Pierre à Rome.
L’image suivante présente une mosquée de la ville de Kirman, en Iran. L’intérêt de cette image est de nous présenter, sur le toit de la mosquée, un panel de figure conservées par des groupes diédriques. Le plus grand de ces groupes est, semble-t-il, D22.
Enfin, voici les arenes de Nîmes, en France. Le groupe diédrique qui conserverait ces arenes serait bien plus grand que D22, si toutefois cette forme était circulaire, et non ellipsoïdale comme le sont toutes les arenes.

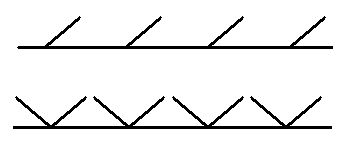
Nous avons présenté plus haut les symétries de
rotations du groupe cyclique Cn et du groupe diédrique D2n qui conservaient un n-gone régulier convexe. Dans le cas
infini, ces groupes de rotations deviennent des groupes de translations. Voici une
représentation graphique des groupes C![]() et D
et D![]() .
.
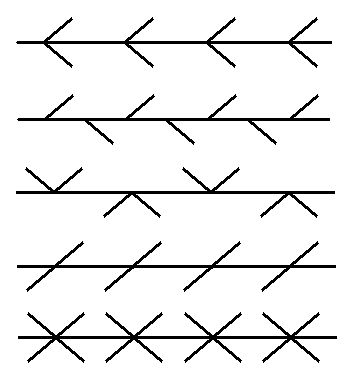
Un groupe H d’isométries de E2 est appelé groupe de frises si le
sous-groupe de translations de H est engendré par une translation (différente de
l’identité), c’est à dire si le sous-groupe des translations est cyclique
(nécessairement infini). Tout ensemble de points du plan E2 tel que le groupe
des isométries qui le conserve est un groupe de frises est appelé frise. Il n’y a
que 7 types de frises non-isomorphes. Les deux premiers types correspondent à C![]() et D
et D![]() . Voici les 5 autres
types.
. Voici les 5 autres
types.
Aucun monument ne pourrait représenter un groupe de frises (par définition infini): nous devons nous contenter de reproduire partiellement ces symétries, et laisser à notre imagination le soin de représenter ces batiments s’ils avaient une longueur infinie.
Nous avons à peine parlé de la musique. Cet art contient cependant un parfait exemple de symétrie de translation. La frise, dans la musique, c’est le rythme.
| Université Libre de Bruxelles | MATsch - gdemeur @ ulb.ac.be (sans les espaces) |
Mise à jour: Novembre 2000 |