
Les mathématiques
dans la nature,
les nombres de Fibonacci
 |
Les mathématiques
dans la nature, |
Contenu de ce document
Un exemple de nombres de Fibonacci dans la nature inorganique
On fait traverser par un rayon lumineux deux plaques de verre collées entre elles. Lorsque le rayon quitte une plaque de verre, il se réfléchit en partie. Nous comptons les trajectoires possibles des rayons émergents pour un nombre de réflexions données.
| Nombre de réflexions | Nombre de trajectoires | Schéma |
| 0 | 1 |
|
| 1 | 2 |
|
| 2 | 3 |
|
Et pour 3 réflexions, 4 trajectoires? Pas si simple!
La première idée est de rajouter aux cas traités de 2 réflexions, une troisième réflexion en D. Toutefois, pour les deux premiers dessins de ce cas, la troisième réflexion peut déjà se produire en B. En observant le schéma du haut, nous remarquons que ces deux cas correspondent au cas d'une seule réflexion à laquelle on rajoute une deuxième réflexion en A et une troisième réflexion en B. Au total, nous avons donc 3 + 2 = 5 trajectoires pour le cas de 3 réflexions.
| Nombre de réflexions | Nombre de trajectoires | Schéma |
| 3 | 5 trajectoires = 3 trajectoires à partir du cas de 2 réflexions + 2 trajectoires à partir du cas de 1 réflexion |
|
Cette méthode de dénombrement se généralise: le nombre de trajectoires pour un cas donné de réflexions correspond au nombre de trajectoires du cas précédent auquel nous rajoutons une réflexion en quittant les plaques, plus le nombre de réflexions du cas antépénultième auquel nous rajoutons une réflexion à l'intersection des deux plaques et une réflexion en quittant les plaques.
Ainsi le nombre de trajectoires pour 4 réflexions est
5 (cas de 3 réflexions + 1
réflexion en A)
+ 3 (cas de 2 réflexions + 1 réflexion en D + 1
réflexion en C)
= 8 trajectoires.
Le nombre suivant sera 8 + 5 = 13.
Puis 13 + 8 = 21.
Etc.
Le nombre de trajectoires pour n réflexions est la somme du nombre de trajectoires pour (n-1) réflexions et du nombre de trajectoires pour (n-2) réflexions. Si Fn correspond à ce nombre, nous écrivons
Fn = Fn-1 + Fn-2
La données de deux valeurs initialles F0 et F1 détermine une suite. En choisissant
F0 = 0 et F1 = 1,
la suite construite est celle de Fibonacci, et le nombre Fn est appelé nième nombre de Fibonacci. Ces nombres ont été découverts (ou inventés?) par Léonard de Pise, dit Fibonacci.
Les premiers nombres de cette suite sont
| F0 = 0 | F5 = 5 | F10 = 55 | F15 = 610 |
| F1 = 1 | F6 = 8 | F11 = 89 | F16 = 987 |
| F2 = 1 | F7 = 13 | F12 = 144 | F17 = 1597 |
| F3 = 2 | F8 = 21 | F13 = 233 | F18 = 2584 |
| F4 = 3 | F9 = 34 | F14 = 377 | F19 = 4181 |
De manière générale, le nième nombre de Fibonacci est donné par la formule

Un couple de lapins conçoit un autre couple un mois après sa propre conception. Le couple de lapinots naît au début du second mois. Nous représentons le couple de lapins par un dessin d'un petit lapin. Le nombre de mois indiqué à sa droite représente l'âge du couple au début du mois. Dénombrons ces couples au début du nième mois.
mois 1 |
mois 2 |
mois 3 |
mois 4 |
mois 5 |
mois 6 |
| 1 couple | 1 couple | 2 couples | 3 couples | 5 couples | 8 couples |
| 1 reproductible | 1 reproductible | 2 reproductibles | 3 reproductibles | 5 reproductibles | |
| 1 non-reproductible | 1 non-reproductible | 2 non-reproductibles | 3 non-reproductibles |
Soit Ln le nombre de couples au mois n. Au mois n, nous retrouvons tous les lapins déjà vivants au mois n-1 (en nombre Ln-1) et leurs enfants; mais seuls ceux reproductifs en (n-1) ont des enfants. Or les reproductifs en (n-1) sont ceux qui existaient en (n-2) (en nombre Ln-2). Ainsi,
Ln = Ln-1 + Ln-2.
Si nous débutons au mois 1 avec un couple de lapins
L1 = 1
au mois 2 avec ce même couple
L2
= 1
nous retrouvons Ln = Fn. Le nombre de couples de lapins au nième
mois est le nième nombre de Fibonacci.
Deux remarques:
Considérons la règle suivante régissant la reproduction d'une colonie d'abeilles. Un mâle donne naissance, en fécondant un oeuf, à une femelle. Une femelle donne naissance à une autre femelle et à un mâle. En débutant avec un mâle, dénombrons les abeilles à la nième génération.
Nous représentons les males par ![]() et les
femelles par
et les
femelles par ![]() .
.
| Génération 1 | Génération 2 | Génération 3 | Génération 4 | Génération 5 | Génération 6 |
| 1 abeille | 1 abeille | 2 abeilles | 3 abeilles | 5 abeilles | 8 abeilles |
| 1 femelle | 1 femelle | 2 femelles | 3 femelles | 5 femelles | |
| 1 mâle | 1 mâle | 2 mâles | 3 mâles |
Nous obtenons le même schéma que pour les lapins. Les couples de lapins reproductifs y sont remplacés par les femelles, et les couples de lapins non-reproductifs y sont remplacés par les mâles. Nous concluons donc que le nombre de d'abeilles à la nième génération est le nième nombre de Fibonacci.
Remarque: Les remarques valables pour les couples de lapins s'appliquent pour les abeilles. Elles traduisent le fait que le nombre de femelles à la nième génération, ainsi que le nombre de mâles, suivent eux-aussi la suite de Fibonacci.
Nous quittons les raisonnements mathématiques et les exemples assez fictifs pour entrer dans le domaine de l'exemple visuel de la beauté de la nature.
La phyllotaxie, la botanique, les spirales
La phyllotaxie est la branche de la botanique qui étudie la disposition des feuilles d'une branche sur la tige. pour p tours autour de la tige, nous comptons q le nombre de feuilles rencontrées. Les quotients p/q ont tendance à approcher les suites de Fibonacci: 1/2 1/3 2/5 3/8 5/13 8/21 ... Toutefois, nous rappelons qu'aucun raisonnement mathématique ne justifie ce résultat. Seule l'observation, et donc la statistique, permet de retrouver ces nombres. |
 |
Quand nous regardons le coeur d'un tournesol, nous remarquons que les fleurons qui le composent forment deux familles de spirales. Une première famille qui s'éloigne du centre dans le sens horloger, et une seconde famille dans le sens anti-horloger.
 Coeur d'un tournesol |
 Coeur d'une marguerite |
Chaque fleuron constitue l'intersection d'une spirale de chaque famille. Structure remarquable du coeur de tournesol. Lorsque la nature n'a pas créé un mutant, le nombre de fleurons des spirales du premier type et le nombre de fleurons des spirales du second type sont constants, et sont deux nombres adjacents de la suite de Fibonacci.
34 dans un sens et 55 dans l'autre.
55 dans un sens et 89 dans l'autre.
...
Il n'est pas nécessaire de se procurer un tournesol pour vérifier ce phénomène de visu. Il suffit de la vérifier sur des pommes de pin ou des ananas. Le résultat est surprenant.
 Cactus |
 Pomme de pin |
Soit un carré de côté 1. On construit à son côté un autre carré de côté 1. Nous formons ainsi un rectangle. Ensuite on enroule une succession de carrés basés sur le plus grand côté des rectangles successifs ainsi formés.
 |
 |
 |
images originales issues du site http://www.ee.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
Les longueurs successives des côtés des carrés dessinés
constituent, par construction, la suite de Fibonacci. Le rapport avec la nature? Il
apparaît lorsque nous dessinons dans chaque carré un quart de cercle centré au sommet
du carré le plus proche du carré initial, et dont le rayon vaut le côté du carré
dessiné. Nous dessinons ainsi une spirale proche de la spirale appelée spirale
exponentielle ou spirale logarithmique. L'équation polaire d'une spirale logarithmique
est très simple puisqu'elle exprime que l'angle polaire ![]() d'un point de la courbe est un multiple
du rayon polaire r.
d'un point de la courbe est un multiple
du rayon polaire r.
| r = a exposant |
Nous venons de décrire une apparition d'une spirale "cousine" dans le coeur de tournesol. Cette spirale logarithmique se retrouve elle aussi dans la nature avec, comme exemple le plus représentatif, la coquille du Nautilus Pompilius.
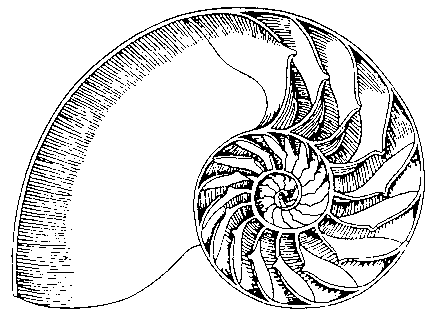
Nous retrouvons ces formes spiralées sur multitude de coquilles calcaires de mollusques, escargots, ...
Léonard de Pise naît en 1170, vraisembleblement à Pise. Son père occupant un poste diplomatique, il le suit très tôt à l'étranger et reçoit son éducation en Afrique du Nord. Durant ces voyages, il s'intéresse et accumule quantité de données sur les systèmes mathématiques de ces pays. De retour en Italie en 1202, il publie ces données dans "Liber Abaci". Cet ouvrage introduit au monde européen les nombres arabes, ainsi que le système de positionnement décimal arabe-hindou. C'est aussi à l'occasion de cet ouvrage qu'il introduira les nombres et la suite étudiée sur cette page. Son nom est aujourd'hui retenu presque exclusivement pour cette suite. Toutefois, Fibonacci nous a aussi livré des notions de géométrie et de trigonométrie. Citons parmi ses ouvrages "Mis Practica Geometriae" en 1220 et "Liber Quadratorum" en 1225. Léonard de Pise est mort en 1250, sans doute à Pise. Aujourd'hui, la revue "Fibonacci Quarterly" publie dans chaque numéro des problèmes mathématiques faisant intervenir sa fameuse suite.
| Université Libre de Bruxelles | MATsch - gdemeur @ ulb.ac.be (sans les espaces) |
Mise à jour: Novembre 2000 |