
Le rectangle des
Kariera
 |
Le rectangle des
Kariera |
|
|
En Australie, en Afrique équatoriale, en Amérique du Sud, ou en Asie du sud-est, certaines sociétés "traditionnelles" - de nos jours le terme primitif est devenu politiquement incorrect, au détriment de la richesse de son sens premier - ont pratiqué des règles de mariage et de filiation prescriptifs . La société y est divisée en sous-ensembles disjoints - aussi nommé "classes" ou "sections" par les ethnologues- qui fondent les règles régissant la parenté. Chaque individu appartient à une seule classe, chacun(e) doit choisir son époux(se) au sein d’une autre classe déterminée et aura ses enfants dans une autre classe également fixée. Les règles dépendent évidemment de la société considérée, mais certaines d’entre-elles possèdent des propriétés communes qui permettent d’en étudier les "invariants" grâce à la théorie des groupes. Ces propriétés communes peuvent s’énoncer sous forme d’axiomes qui serviront à définir le modèle mathématique sous-jacent à ces sociétés. Une fois défini, ce modèle pourra être étudié mathématiquement, sans plus devoir recourir aux formes concrètes qui lui ont donné naissance; on pourra ainsi découvrir des propriétés générales valables pour toutes les sociétés ainsi modélisées, démontrer des théorèmes les concernant, lister des cas possibles, rechercher des ressemblances, expliquer des régularités observées, en prédire d’autres...
Successivement, les thèmes suivants sont proposés, mais il est loisible d’adopter un autre ordre de lecture, en cliquant sur les mots-clés (soulignés) des titres de paragraphes:
Sois mon parent ... ou mon ennemi !
Les règles de mariage et de filiation exposées ici se comprennent mieux lorsqu’on s’est familiarisé avec la "parenté classificatoire"; pour une société qui voit la parenté selon ce schéma, chaque individu est repérable soit comme "parent" soit comme étranger, et donc ennemi. L’ensemble des "parents" c’est la société même. Une citation de Radcliffe Brown, traduite dans Les structures élémentaires de la Parenté de C.Lévi-Strauss ([...]p.52-53) relate cet état d’esprit en ces termes:
"Quand un étranger approche d'un camp qu'il n'a jamais visité auparavant, il ne pénètre pas dans le camp, mais se tient à quelque distance. Après un moment, un petit groupe d'anciens l'aborde, et la première tâche à laquelle ils se livrent est de découvrir qui est l'étranger. La question qu'on lui pose le plus souvent est : Qui est ton maeli (père du père)? La discussion se déroule sur des questions de généalogie, jusqu'à ce que tous les intéressés se déclarent satisfaits, quant à la détermination exacte de la relation de l'étranger avec chacun des indigènes présents au camp. Quand on est arrivé à ce point, l'étranger peut être reçu dans le camp, et on lui indique chaque homme et chaque femme, avec la relation de parenté correspondante entre lui-même et chacun ... Si je suis un indigène et que je rencontre un autre indigène, celui-ci doit être, ou bien mon parent, ou bien mon ennemi. Et s'il est mon ennemi, je dois saisir la première occasion de le tuer, de crainte que lui-même ne me tue."
A. R. RADCLIFFE BROWN, Three Tribes of Western Australia,
Un exemple concret : la société KARIERA
| Se fondant sur des textes de Radcliffe Brown, C. Lévi-Strauss décrit comme suit le
fonctionnement d’un groupe tribal que l’on retrouverait dans l’Ouest et
dans l’Est de l’Australie: "Les KARIERA appartiennent à l'une ou à
l'autre des sections suivantes: BANAKA, KARIMERA, BURUNG, PALYERI. |
 |
Un petit dessin valant un grand discours, on « traduira » cette description par le schéma suivant:
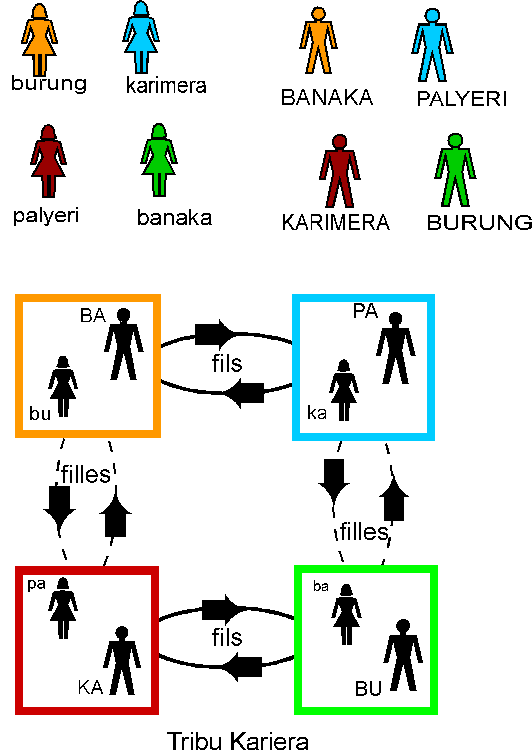
on y remarque d’emblée 4 types de mariage, que l’on peut désigner respectivement par (buBA), (baBU), (kaPA) et (paKA), avec la convention (minuscule=femme) et (majuscule=homme). La structure révèle aussitôt ses symétries ainsi que ses cycles. Les voyez-vous?
Une axiomatique des "groupes de parenté"
Bref traitement mathématique du modèle
Tous les possibles dans un monde coupé en quatre
Et quand les temps sont durs...
En fait, assez peu ! L’étude des "groupes de parenté", et plus généralement la formalisation mathématique n’est pas vraiment à la mode dans les travaux anthropologiques récents; en 1985 Elaine Lally avait cependant réalisé une bibiographie commentée de 207 entrée sur le sujet...sans prétention d’exhaustivité. Il est d’ailleurs intéressant d’en lire quelques travaux fondateurs, comme l’appendice d’André Weil sur le système Murngin, la formalisation de Guilbaud, de Courrège, celle de Kemeny, l’entreprise classificatoire de White, puis celle plus récente de Liu:
P. COURREGE , « Un modèle mathématique des structures de parenté », L'Homme, (1965), 5.
G.Th.GUILBAUD, « Système parental et matrimonial au Nord Ambrym », Journal de la société des Océanistes 26 XXVI (mars 1970).
J.KEMENy, J.SNELL, G.THOMPSON, « Algèbre moderne et activité humaine, Dunod, Paris (1960 pour la traduction française)
Pin-Hsiung Liu, Foundations of Kinship Mathematics
A. WEIL, « Sur l’étude algébrique de certains types de lois de mariage », in Lévi-Strauss , Paris, Mouton, (1949)
H. C . WHITE, « An anatomy of kinship », Prentice Hall ( 1963).
Certains auront éventuellement la curiosité de vouloir connaître ce qui m’a personnellement intéressée dans ce sujet:
« Groupes des systèmes de parenté », G. DE MEUR, Algèbre appliquée et Combinatoire Grenoble ( 1978), 142-149 .
« Attention! Un modèle peut en cacher un autre », G. DE MEUR, in "Mélanges Paul Libois", Bruxelles,1981.
« Une structure pour les Murngin », G. DE MEUR, in "New Trends in Mathemetical Anthropology", ed.G.De Meur, Routledge & Kegan Paul,London,1985,pp.125-138.
« Une représentation homogène de systèmes matrimoniaux,ou l'effacement d'Ego », G. DE MEUR, in: "Les complexités de l'alliance" vol.2 éd. F.Héritier et E.Copet-Rougier, Editions des Archives Contemporaines,Paris,1991.
« Mathématiques et Anthropologie », G. DE MEUR in: "Dictionnaire de l'Ethnologie et de l'Anthropologie", éd. P.Bonte, M.Izard, P.U.F., Paris, 1991.
"La question Murngin, un Artefact de la littérature anthropologique", G. DE MEUR avec P.Jorion, L'Homme,XX(2),39-70, avril-juin 1980.
"A possible Genealogy of Australian Marriages", G. DE MEUR avec P. Jorion Mathematical Social Sciences,2,9-21,(1981).
"Le mariage Pende", G. DE MEUR avec P.Jorion & T.Vuyk, L'Homme XXII(1),53-73,(jan-mars 1982).
D’aucuns se délecteront peut-être davantage des critiques formulées à l’encontre de cette approche formalisée; selon moi, trois d’entre elles se distinguent particulièrement:
| Bien sûr, cette classification n’engage que moi ... à chacun son chat ! |
 |
| Université Libre de Bruxelles | MATsch - gdemeur @ ulb.ac.be (sans les espaces) |
Mise à jour: Novembre 2000 |