La cartographie par projection, technique imparfaite

Observer la Terre sur un globe est une opération agréable, mais peu pratique dès que l’on veut un peu de détail : un globe surdimensionné est trop difficile à manipuler. Il est donc naturel de vouloir représenter la Terre sur des cartes planes. Mais un problème essentiel se pose alors : quiconque a essayé d’écraser la peau d’une orange sur une table a constaté qu’il ne pouvait l’aplanir qu’en la déchirant. En d’autres termes, la surface d’une sphère ne peut être appliquée sur une surface plane sans déchirure ni déformation. Le même problème se pose pour la représentation du ciel étoilé.

Donc, toute carte plane est imparfaite, et ce d’autant plus que la partie de la surface terrestre à représenter est importante. Néanmoins, on dispose, en fonction du mode de représentation choisi, d’une certaine liberté dans le choix des déformations. Or, que demande-t-on à une carte ?

1. D’être équivalente, c’est-à-dire de respecter les proportions dans les surfaces : particulièrement important lorsqu’il s’agit de montrer l’importance respective des différentes régions (cartes géostratégiques et économiques).
2. D’être équidistante, c’est-à-dire de respecter les proportions dans les distances et les surfaces (être à une échelle déterminée) : indispensable pour mesurer les distances sans erreur et choisir le chemin le plus court (cartes pour le voyage terrestre)
3. D’être conforme, c’est-à-dire de respecter les angles et les formes, sans quoi on ne peut reconnaître les continents ou les constellations ; c’est également nécessaire pour déterminer un cap (cartes pour le voyage maritime et aérien)

Les déformations induites par la projection font qu’une carte ne peut avoir à la fois ces trois propriétés : il faut choisir.

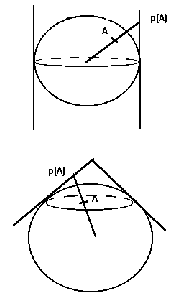
La projection de Mercator, encore très utilisée, est un exemple de projection conforme -logique, quand on considère qu’elle était destinée à la navigation- ; mais il est notoire qu’elle ne respecte absolument pas les surfaces : le Groenland (superficie : un peu plus de 2 millions de km²) apparaît aussi grand que l’Afrique (30 millions). Pour réaliser cette projection, on imagine la Terre enveloppée dans un cylindre qui lui est tangent à l’équateur (fig. 1) et on projette chaque point de la surface sur le cylindre, en partant du centre. La zone la mieux représentée est une bande centrée sur l’Equateur.

La projection conique de Lambert, très utilisée pour la représentation des latitudes moyennes, est également conforme ; elle utilise un cône tangent à la terre selon un parallèle, la projection se fait à partir du centre, sur le cône. (fig. 1) La zone la mieux représentée est une bande centrée sur le parallèle de contact.

Ces deux projections ne sont mathématiquement qu’une seule : en effet, un cylindre peut être vu comme un cône dont le sommet est rejeté à l’infini ; et le parallèle de contact se trouve alors être l’équateur. La projection par le centre ne distingue par fondamentalement entre cône et cylindre (la notion de cylindre, faisant intervenir les parallèles, n’a pas de sens en géométrie projective, les projections ne respectant pas le parallélisme).

Cylindre de Mercator         Cône de Lambert tangent en 60°N

Pour assurer l’équivalence, on peut faire appel à la projection de Peeters ; celle-ci, réalisée perpendiculairement au cylindre tangent eu non à la surface de la terre, fut conçue à l’origine dans un but de "correction politique" : la projection de Mercator, classique dans les Atlas, n’assurait pas la représentation du tiers-monde, proche de l’Equateur, à sa juste valeur et surdimensionnait les régions industrialisées, plus proches des pôles. Mais cette projection tombe dans l’excès contraire : en étirant les continents dans le sens Nord-Sud dans les régions équatoriales, elle surdimensionne par exemple l’Afrique au détriment de l’Europe -sinon en surface, du moins en longueur.

[dessin]

La projection de Mollweide, qui représente la surface de la terre non sous la forme d’un rectangle, mais sous celle d’une ellipse, est équivalente, et ne déforme pas trop ; elle représente donc un honorable compromis ; elle est souvent utilisée pour les cartes de dimension réduite, et pour les représentations de la Galaxie. En effet, elle est assez fidèle dans une large bande autour de l’Equateur, et la Galaxie est fort aplatie.

Il est également possible de réaliser un "élégant" compromis par l’usage de projections aphylactiques, c’est-à-dire qui ne respectent aucune des trois conditions parfaitement, mais sont proches de chacune des trois dans une zone de surface assez large.

Il est cependant des solutions bien plus efficaces ; reprenons donc la phrase de l’introduction : "la surface d’une sphère ne peut être appliquée sur une surface plane sans déchirure ni déformation" : si l’on veut éviter les déformations, pourquoi ne pas admettre les déchirures ?

Première solution : répartir la surface de la terre en plusieurs zones, chacune d’entre elles étant alors projetée selon le mode qui lui convient le mieux. C’est l’objet des projections polygonales. Evidemment, les raccords entre les pièces du puzzle ne sont pas possibles, ou alors au prix de brisures (les lignes qui traversent la zone de jonction se retrouvent brisées). Ainsi, de bonnes cartes du ciel peuvent être réalisées par l’emploi d’une projection de Mercator et de deux projections coniques (cône tangent au 60è parallèle, ou cône sécant à la surface aux 45è et 75è parallèles), ou encore deux projections stéréographiques (à partir du centre, sur un plan tangent au pôle).

... et après tout, un Atlas n’est rien d’autre qu’une application de ce principe, avec de nombreuses pièces.

[dessin]

Seconde solution : celle du canevas de Goode et de quelques autres systèmes, qui acceptent de déchirer la surface terrestre au moment de la projection, comme celle de l’orange, en s’arrangeant pour que le plus clair des déformations se produise au beau milieu des océans : si l’on a en tête la représentation des continents et d’eux seuls, c’est certainement la solution la plus adéquate. On profite du fait que les continents ne sont guère larges au sud de l’Equateur, et on provoque les déchirures entre eux.

pour en savoir plus ...

la Cartographie, in Encyclopedia Universalis vol. 5, pp. 24-32, F. JOLY et G. BONNEROT.

la Cartographie, P.U.F. - Que sais-je?, F. JOLY, Paris 1985.

les systèmes de projection et leurs applications, F. REIGNIER, IGN, Paris 1957.