
Les ponts
suspendus
 |
Les ponts
suspendus |
L’idée même de ponts suspendus est probablement née dans les forêts tropicales encombrées de lianes géantes, particulièrement sur les pentes indiennes et chinoises des contreforts de l’Himalaya. En 1858, Freeman décrivit, croquis à l’appui, le pont Srinagar dans le Cachemire. Celui-ci, entièrement construit à l’aide de filaments d’un arbre des montagnes, permettait de franchir les 73 mètres séparant les rives du fleuve. En Chine, on recense des passerelles suspendues au-dessus de profonds ravins ou de gorges. Constituées par la succession de planches en bois fixées transversalement à des chaînes en fer forgé, certaines auraient même plus de 2000 ans d’existence! Concernant l’Europe, la mention la plus ancienne remonterait à 1515. Il s’agit de ponts de cordes utilisés lors des campagnes militaires. Du fait de son aspect plutôt éphémère, ce type d’ouvrages fut certainement beaucoup plus courant que l’Histoire n’en a conservé la trace.
La présence de ponts suspendus d’une longueur étonnante au sein même de sociétés à tradition orale d’Afrique, d’Océanie et d’Amérique du Sud, semble confirmer que leur capacité à enjamber de grandes distances ait été de tout temps reconnue. En plus d’être légers, ils sont faciles et rapides à construire. Malheureusement, lorsqu' une personne se déplace sur un tel pont de cordes, la flexibilité importante de ce dernier entraîne inévitablement des oscillations verticales couplées souvent à un balancement latéral, et ce même en l’absence de vent. En outre, ces ouvrages primitifs ne peuvent supporter des charges lourdes ou concentrées.
Quand les points d’attache d’une corde (chaîne, câble, fil, ..... ) sont situés à la même hauteur et que cette corde n’est guère plus longue que la portée, la courbe décrite semble être identique à un arc de parabole. Toutefois, ce n’est qu’en 1690 que J. Bernouilli démontrera que ce n’est pas le cas. Le paragraphe qui suit fait intervenir des notions de statique, conduisant à la résolution d'une équation différentielle du second degré. Voilà pourquoi, si l'aspect "calcul" vous rebute, nous vous conseillons de vous reporter immédiatement au résultat final.
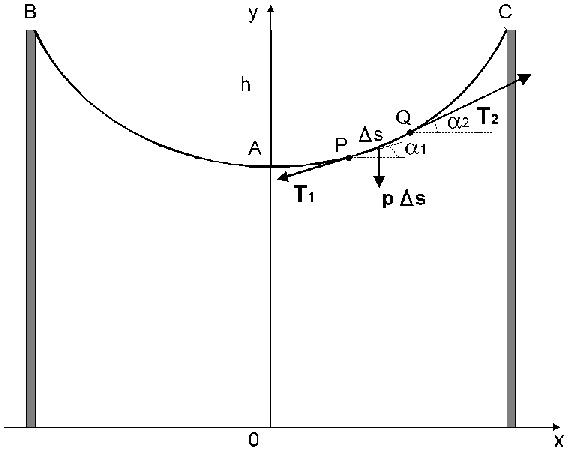
Considérons un fil flexible de longueur 2L, suspendu à ses deux
extrémités B et C, et soit p son poids par unité de longueur. Puisque le fil est
sans raideur, les forces de tension T sont, en tout point, tangentes au fil. Soit
un élément PQ = ![]() s
de ce fil. S’il y a équilibre des forces, la tension T1 en P, la
tension T2 en Q et le poids p
s
de ce fil. S’il y a équilibre des forces, la tension T1 en P, la
tension T2 en Q et le poids p ![]() s de cet élément PQ ont une résultante
nulle, ce qui revient à dire que:
s de cet élément PQ ont une résultante
nulle, ce qui revient à dire que:
| selon 0x: T2 cos a 2 - T1 cos a 1 = 0 | (1) |
| selon 0y: T2 sin a 2 - T1
sin a 1 - p |
(2) |
P et Q étant quelconques, nous déduisons de (1) que la coordonnée suivant l'axe 0x de la tension est constante en grandeur en tout point du fil et correspond donc à T0 la tension en A, point le plus bas de la courbe.
![]() T2 cos a 2 = T1 cos a 1 = T0
T2 cos a 2 = T1 cos a 1 = T0
(2) devient donc:
tg a 2 - tg a 1 = p![]() s / T0
s / T0 ![]()
![]() tg a /
tg a / ![]() s = p / T0 (3)
s = p / T0 (3)
Faisons tendre Q vers P, et posons T0 / p = a
(3) devient alors:
dtg a / ds = 1/ a ![]() a. d(dy/dx) / dx = ds/dx
a. d(dy/dx) / dx = ds/dx ![]() a. d2y/dx2 = [ 1+
(dy/dx)2 ]1/2 (4)
a. d2y/dx2 = [ 1+
(dy/dx)2 ]1/2 (4)
Pour résoudre cette équation différentielle, posons k = dy/dx
(4) devient:
a. dk/dx = (1+k2 )1/2 ![]() a. (1+k2 )-1/2
dk = dx (5)
a. (1+k2 )-1/2
dk = dx (5)
Intégrons (5):
a. ln [ k + (1+k2 )1/2 ] = x + C
Comme k = 0 pour x = 0, nous avons donc
C = 0 => k + (1+k2 )1/2 = ex/a (6)
En remplaçant x par -x, il faut remplacer k par -k et (6) devient alors:
-k + (1+k2 )1/2 = e-x/a (7)
(6) et (7) => k = 0,5 . ( ex/a - e-x/a
) ![]() y = 0,5 a .
( ex/a + e-x/a ) + C’
y = 0,5 a .
( ex/a + e-x/a ) + C’
La position de l’axe 0x étant arbitraire, convenons de prendre a pour ordonnée du point A, ce qui donne C’= 0
=> y = 0,5 a . ( ex/a + e-x/a ) = a . Ch x/a (8)
De même, il est possible de montrer que a = (L2 - h2 ) / 2h , où h représente la distance, encore appelée flèche, entre l’horizontale passant par les points d’attaches du fil et le point le plus bas de la courbe. L’équation n° (8) correspond à la figure d’équilibre d'une Chaînette. Notons que le poids propre d’un arc inextensible ayant une telle forme n’influence pas sur la flèche. Suivant la longueur du fil et la distance entre les points B et C (ces deux paramètres déterminant la valeur h de la flèche), le fil adoptera des formes différentes, mais ces dernières resteront toujours des arcs de chaînette!
De nombreux exemples illustrent à merveille la présence de la chaînette dans notre environnement quotidien et ce de manière parfois assez inattendue:
Si le premier pont "civil" qui ait plus directement inspiré les ponts suspendus modernes fut érigé en Angleterre vers 1741, c’est néanmoins à l’Américain J. Finley que revient la paternité du premier pont suspendu de l’ère industrielle, réalisé en 1801. Finley devait répondre à moindre coût aux problèmes de franchissement posés par des rivières et des fleuves d’une largeur peu commune en Europe.
Peu onéreuse, permettant la réalisation de portées considérables sans appui intermédiaire, la technique du pont suspendu fera très vite fureur en Europe. En effet, à cette époque, la science de l’ingénieur y était plus poussée qu'aux Etats-Unis. Parallèlement à cela, une nouvelle approche de l'esthétique des ponts, liée aux concepts de transparence et de légèreté, fera son apparition. Les principaux partisans des ponts suspendus seront les frères Seguin en France et le Suisse G.H. Dufour. Toutefois, vers 1850, suite à plusieurs catastrophes comme celle du pont d'Anger ou celle de la Roche-Bernard, les Européens vont se tourner vers d’autres types de ponts, réputés plus solides, contrairement aux Américains qui eux vont persévérer dans cette voie.
Les premiers ingénieurs faisant véritablement figure de pionniers aux Etats-Unis furent C.Ellet et les Roebling père et fils. En 1852, ces derniers construisirent le premier pont suspendu pour voie de chemin de fer, au dessus de la rivière Niagara, en amont des chutes. De 1867 à 1883, ils bâtirent le pont de Brooklyn sur l’East River. En introduisant l'acier, ils arrivèrent à une meilleure maîtrise du phénomène de corrosion des câbles, câbles qui se substituèrent rapidement aux chaînes métalliques à maillons plats. Ils tentèrent aussi de remédier à la trop grande souplesse des tabliers d'ouvrages suspendus, par l'ajout de câbles rectilignes inclinés et d'une poutre de rigidité longitudinale.
Un pont suspendu comporte trois parties essentielles à savoir, les tours, les ancrages et les câbles. Les armatures de renforcement et la chaussée peuvent être partiellement ou totalement détruites sans causer l'écroulement du pont dans son entièreté. Les matériaux utilisés pour la construction des tours sont la pierre de taille, l'acier et le béton armé pour les pylônes les plus récents. Leur hauteur dépend de la flèche adoptée pour les câbles porteurs, flèche qui pour une raison d'économie maximum doit être comprise entre 1/8 et 1/12 de la longueur de la travée principale (espace compris entre les deux tours). Les ancrages ayant pour fonction de sécuriser les extrémités des câbles, leur poids constitue un facteur fondamental. C'est pourquoi ils sont généralement réalisés en béton ou en maçonnerie sauf dans certains endroits favorisés où il est possible d'ancrer les câbles immédiatement dans la roche naturelle. Les câbles porteurs, élément clef de l'ouvrage, supportent le poids du tablier et donnent à la structure son caractère. Ils sont constitués par l'assemblage en parallèle de fils en acier du diamètre d'un crayon, ou de plusieurs torons de fils enroulés en spirale.
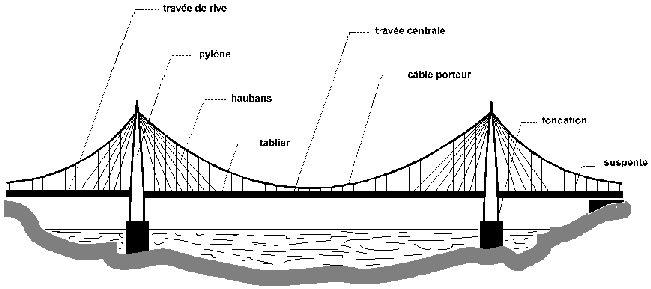
Si la chaussée est directement attachée aux câbles porteurs par des suspentes, la structure manque de rigidité et le pont suspendu apparaît dès lors comme une sorte de balançoire, sensible aussi bien à l'action de la circulation (véhicules, passage de trains, défilés militaires au pas cadencé, .....) qu'à celle du vent ou de la pluie. La mise en résonance d'un pont supendu peut survenir lorsqu'une fréquence propre de l'ouvrage se voit excitée par l'une ou plus des charges dynamiques appliquées.
Les phénomènes dynamiques engendrés par l'action du vent sur une structure souple peuvent être répertoriés en deux catégories: l'excitation directe de la structure par des vents extrêmes et aléatoires d'une part, et l'excitation par des vents relativement modérés mais sensiblement constants d'autres part, pouvant prendre diverses formes, une excitation verticale du tablier par échappement tourbillonnaire alterné ou des oscillations auto-entretenues à un (galop) ou plusieurs (flottement classique) degrés de liberté. De telles vibrations induites sont à l'origine de nombreuses défaillances dont la plus célèbre reste celle du Tacoma-Narrows Bridge près de Seattle; ce pont s'écroula le 7 novembre 1940 alors que la vitesse du vent n'était pas excessive (18,71 m/s), mais celui-ci avait soufflé régulièrement durant les deux heures précédant la catastrophe. Le principal défaut du Tacoma-Narrows était sa poutre de rigidité à âme pleine, située sous la chaussée, qui offrait une trop grande prise au vent.
Pour éviter cet inconvénient, les Américains remplacèrent ce type de poutre par un treillis métallique résistant à la fois en flexion et en torsion. Cette armature de plusieurs mètres de hauteur est accrochée aux câbles porteurs et distribue les charges dynamiques concentrées sur une longueur considérable du câble.
Constatant que l'usage d'un treillis rigide, en plus d'enlaidir considérablement l'ouvrage, ne réduisait nullement l'emprise du vent sur le pont, les Européens trouvèrent plus judicieux de limiter au maximum cette emprise, via une conception plus aérodynamique du tablier, empêchant de ce fait la formation de turbulences. Dans les ponts suspendus récents, le tablier métallique à dalle orthotrope (tôle en acier, de ± 20 mm d'épaisseur, raidie selon deux directions perpendiculaires), dont la section transversale a été testée en soufflerie, a remplacé le tablier en treillis. Cette évolution traduit la suprématie actuelle de la technique britannique dans le domaine. L'utilisation de haubans (câbles stabilisateurs rectilignes raccordant le tablier aux pylônes) et d'amarres extérieures, couplée à l'inclinaison du plan des câbles porteurs, créatrice d'un effet "treillis", permet de lutter efficacement contre les phénomènes d'instabilité. Des ponts à câble porteur unique ont également vu le jour: les oscillations en torsion, engendrées par des déformations différentielles entre les deux câbles porteurs, disparaissent complètement.
Le rôle essentiel du système porteur est de transmettre aux appuis les efforts en tension qu'il reçoit des charges permanentes (ex. le poids du tablier), des charges d'exploitation (ex. le trafic routier ou/et ferroviaire), ainsi que des déformations imposées à l'ouvrage (ex. l'action du vent). Quelle est la courbe adoptée par un câble porteur ? Nous allons démonter qu'il prend la forme d'un arc de parabole.
En première approximation, supposons le tablier sans raideur ni flexion particulières, et les pylônes rigides. Le poids d'un câble porteur étant négligeable par rapport à celui du tablier, nous l'assimilerons à un fil inextensible et flexible. Nous retiendrons uniquement l'action des charges permanentes, à savoir que le câble supporte une charge constante et uniformément répartie suivant l'horizontale. Le problème est donc similaire au précédent, sauf que le poids de l'élément D s n'est plus pD s mais bien pD x où p représente le poids du tablier par unité de longueur horizontale.
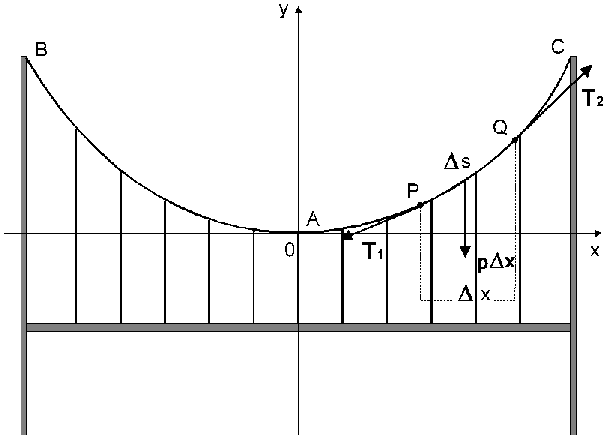
(1) devient:
d(dy/dx) / dx = a ![]() d2y/dx2 = a
(2)
d2y/dx2 = a
(2)
Intégrons (2):
dy/dx = a.x + C (3)
Comme dy/dx = 0 pour x = 0, nous avons donc C = 0
Intégrons (3):
y = 0,5 a.x2 + C' (4)
La position de l'origine des axes étant arbitraire, nous conviendrons de placer celle-ci en A, point le plus bas de la courbe, ce qui donne C’= 0
=> y = 0,5 a . x2 (5)L'équation de la courbe d'équilibre est donc une parabole dont l'axe coïncide avec celui des y.
Depuis le milieu du 19ème siècle, nous assistons à une véritable surenchère concernant le dimensionnement des ouvrages à câbles porteurs paraboliques. Actuellement, les plus longues travées de pont au monde sont toutes de type "suspension":
| Pont suspendu | Année d'inauguration | Portée de la travée centrale | Pays |
| Cincinnati | 1866 | 322 m | Etats-Unis |
| Brooklyn | 1883 | 486 m | Etats-Unis |
| George Whashington | 1931 | 1067 m | Etats-Unis |
| Golden Gate | 1937 | 1280 m | Etats-Unis |
| Verrazano-Narrows | 1965 | 1298 m | Etats-Unis |
| Humber | 1979 | 1410 m | Angleterre |
| Storebaelt | 199.. | 1624 m | Danemark |
| Akashi Kaikyo | 199.. | 1990 m | Japon |
Pour vous donner une petite idée du gigantisme de ces constructions, voici quelques caractéristiques principales du Verrazano-Narrows Bridge de New York:
| Longueur de la structure suspendue | 2038 m | Nombre de câbles porteurs | 4 |
| Portée de la travée centrale | 1298 m | Longueur d'un câble | 2195 m |
| Largeur du pont (entre les câbles) | 31 m | Diamètre d'un câble | 91 cm |
| Hauteur des tours au-dessus des eaux | 210 m | Nombre de fils d'acier par câble | 26108 |
| Hauteur libre au centre du pont | 69 m | Nombre de torons par câble | 61 |
| Fondation la plus profonde sous l'eau | 52 m | Masse des fils dans les câbles | 38500 tonnes |
Enfin, nous aimerions clôturer ce bref tour d'horizon des ponts suspendus en mentionnant les ponts "habités", dont le plus connu est sans conteste le Tower Bridge de Londres, inauguré sur la Tamise en 1894. Les tours de style néogothique renferment le mécanisme hydraulique servant au relèvement de la travée centrale, tandis que les travées de rive sont suspendues à des câbles porteurs paraboliques. Depuis 1982, un musée y a été aménagé.
Références:
(1) A. Bernard-Gély, J-A. Calgaro, Conception des Ponts, Presses de l'école nationale des Ponts et chaussées, 1994
(2) Construire en Acier, Le Moniteur, Paris, 1993
(3) Rassegna, Inhabited Bridges, CIPIA Publisher, 1991
(4) B. Marrey, Les Ponts Modernes: 18ème - 19ème siècles, Picard, 1990
(5) E. Heinle, F. Leonhardt, Tours du monde entier, Livre Total, 1989
(6) J.L. Synge, B.A. Griffith, Principles of Mechanics, McGraw-Hill, 1987
(7) F. Leonhardt, Ponts: L'esthétique des ponts, Presses polytechniques romandes, 1986
(8) D. Jacobs, A.E. Neville, Bridges, Canals and Tunnels, American Heritage Publishing, 1968
(9) E.M. Young, L. Réthi, The Great Bridge: The Verrazano-Narrows Bridge, Farrar, Straus & Giroux, 1965
(10) F. Bultot, Eléments de mécanique rationnelle à l'usage des électroniciens, Gauthier-Villars, 1961
(11) D. Steinman, Bridges and their Builders, Dover Publications, 1957
(12) Y. Rocard, L'instabilité en mécanique: automobiles, avions, ponts suspendus, Masson, 1954
| Université Libre de Bruxelles | MATsch - gdemeur @ ulb.ac.be (sans les espaces) |
Mise à jour: Novembre 2000 |