
Les courbes de
diamètre constant
Les lavabos
 |
Les courbes de
diamètre constant |
Vous êtes-vous déjà demandé pourquoi les bondes de nos lavabos sont toujours rondes, plutôt que carrées par exemple ?
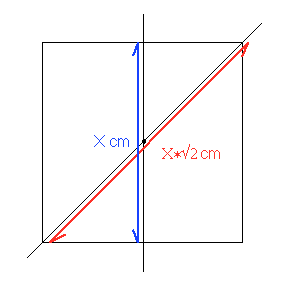
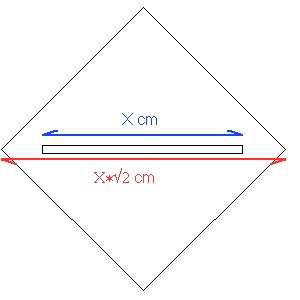
Prenez une bonde carrée de 2 cm de côté. Elle devrait entrer dans un trou qui a la même forme. Mais, si elle entrait dans le trou par la tranche le long de la diagonale ... elle tomberait dans le trou.
Ceci est causé par le fait que les différentes droites passant par le centre de gravité d’un carré coupent le carré selon des segments de longueur différente
 |
 |
Pour éviter que la bonde ne s’échappe par la tuyauterie, il faut donc lui donner - ainsi qu’à son alvéole - la forme d’une courbe de diamètre constant (indépendant de la direction). Les courbes planes (fermées et convexes) de diamètre constant sont parfois appelées figures de Reulaux. La plus simple de ces courbes est le cercle.
Immédiatement après le cercle, la courbe de largeur constante la plus simple se construit en menant, par chaque sommet d’un triangle équilatéral, un arc de cercle passant par les deux autres sommets :
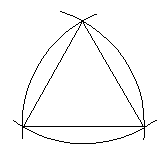
Placée dans un cercle de même diamètre et de même centre, la courbe détermine trois lunules de même forme, sans communication entre elles, et ce, quelle que soit son orientation exacte.
Cette propriété l’a fait utiliser dans les moteurs à explosion de type Wankel (pistons rotatifs), où les différentes phases du cycle du moteur se produisent simultanément dans les différentes chambres délimitées par le piston central. Pour assurer l’efficacité du cycle, il ne peut à aucun moment y avoir de communications entre les chambres. En tournant, le piston fait passer chaque chambre successivement en face de la tubulure d’admission, de la bougie et de la tubulure d’échappement.
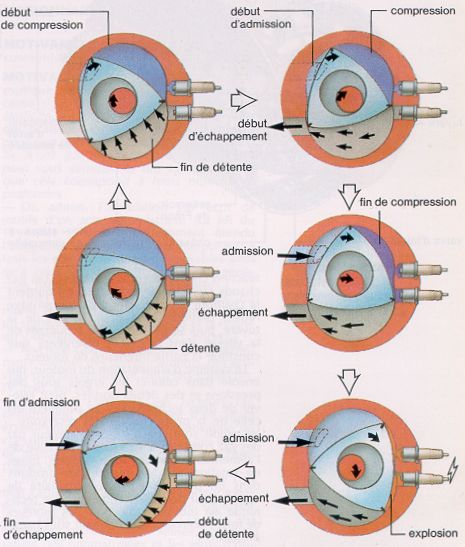
On remarquera que le cylindre n’est pas exactement circulaire, ce qui fait varier la taille des chambres. Ceci est volontaire: la compression est ainsi assurée de par le simple mouvement du piston.
| Université Libre de Bruxelles | MATsch - gdemeur @ ulb.ac.be (sans les espaces) |
Mise à jour: Novembre 2000 |