Designs et compétitions sportives

Supposons que vous organisiez une compétition quelconque : manifestation sportive, comparaison de produits d’entretien, de procédés thérapeutiques, ... et que vous désiriez tester tous les compétiteurs les uns contre les autres.

Il y a plusieurs manières de procéder :

1. Faire concourir tout le monde en même temps, comme cela se fait pour un marathon. Inconvénient : on ne dispose pas toujours de l’espace et du matériel nécessaire pour ce faire.

2. Organiser des rencontres par paires : la seule manière de procéder lorsque l’affrontement est direct à un contre un (échecs). Inconvénients : le nombre de rencontres augmente rapidement avec le nombre de concurrents ( ½(n²-n), où n est le nombre de concurrents), et dans le cas d’une compétition sportive, les efforts répétés peuvent poser un problème aux concurrents.

3. Organiser des éliminatoires ; mais on peut prouver que le résultat final dépend souvent de l’ordre dans lequel les éliminatoires sont organisées ; si l’on veut aboutir à un classement objectif, l’écueil est de taille.

4. Le meilleur compromis peut être d’organiser un nombre limité de sessions, avec un nombre limité de concurrents par session, de manière à ce que chaque paire de concurrents se retrouve une et une seule fois dans une même session. En termes mathématiques, ceci revient à trouver, au sein d’un ensemble E de v points, une famille de sous-ensembles, nommés blocs, chaque bloc comprenant un nombre k d’éléments de E, de telle manière que deux points donnés appartiennent à un même sous-ensemble (et un seul). Une telle structure s’appelle un système de Steiner ou 2-design de Steiner, généralement noté S(2,k, v). On notera b le nombre de blocs.
   
   Chaque concurrent participera alors à un nombre fixe (v-1)/k d’épreuves.
   
   Remarquons qu’il faut forcément avoir : v .(v-1)/k = b .k   ; en effet, le nombre de paires (concurrent - épreuve à laquelle il participe) est égal au nombre de paires (épreuve - concurrent qui y participe).

Le plan affin de 9 points AF(3,2).

Soit 9 points disposés en carré comme ci-dessous :

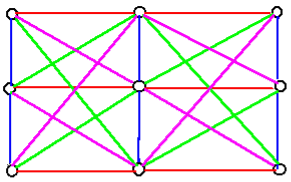
L’ensemble des 9 points et des 9 "droites" (lignes droites ou brisées de couleur uniforme) forme ce que l’on appelle le plan affin de 9 points, ou plan affin sur le corps {0,1,2}. Ses points peuvent être repérés par deux coordonnées prises au sein de l’ensemble {0,1,2}, et les caractéristiques des points et droites sont celles d’un plan affin classique :

• chaque paire de points est sur une et une seule droite ;
• deux droites se coupent en au plus un point ;
• parmi les droites passant par un point n’appartenant pas à la droite A, une et une seule n’a aucun point commun avec A (postulat d’Euclide) ; ...

Les droites ont aussi des équations dont les coefficients sont 0, 1 ou 2 :
          x = a pour les verticales
          y = a pour les horizontales
          x = 2y + a pour les obliques vertes
          y = 2x + a pour les obliques roses
          (a = 0, 1 ou 2)

Ce plan forme un 2-design de Steiner, avec 9 points, 12 blocs (les droites) et 3 points par bloc.

Il est donc possible de faire se rencontrer 9 concurrents en 12 épreuves, chaque épreuve ne comportant que 3 concurrents, de manière que toit le monde concoure contre tout le monde.

Ce plan présente un avantage supplémentaire : les droites d’une même direction (dans la même couleur sur le dessin) forment une partition du plan (chaque point appartient à une et une seule droite de chaque couleur), ce qui permet d’organiser les compétitions en 4 groupes, chaque concurrent participant à une épreuve de chaque groupe (essentiel si des temps de récupération sont nécessaires, ou si des compétitions doivent avoir lieu simultanément en des endroits différents).

Certaines expérimentations (notamment de produits concurrents) sont organisées sur le mode ; il n’est évidemment pas possible de le faire avec n’importe quel nombre de concurrents ; un plan affin a un nombre de points qui est le carré, ou toute autre puissance paire, d’un nombre premier, mais il existe des designs pour de nombreux autres nombres.

C’est également ainsi que sont organisées les compétitions de Speedway , une forme de course pour motos qui se déroule sur un anneau de petites dimensions, ce qui oblige à limiter le nombre de concurrents par épreuve. 16 concurrents participent, et les épreuves sont courues par 4 concurrents. Au bout de 20 épreuves, chaque concurrent en aura disputé 5, et aura couru contre tous les autres.

Comparons avec la variante "tous en piste" (16 concurrents qui se bousculent) ou avec la version "1 contre 1" (120 courses à organiser).

La structure sous-jacente est celle du plan affin AF(4,2), avec 20 droites de 4 points réparties en 5 directions.

Pour plus d’informations sur les designs, avec plus de généralité, on pourra lire :
A.E. BROUWER & H.A. WILBRINK, Block Designs, in Handbook of Incidence Geometry, F. BUEKENHOUT ed., Elzevier 1994.